The Internet is Not As Useful As We May Think
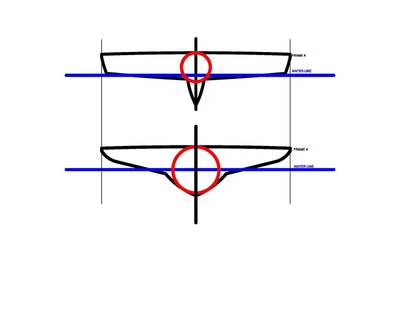
I was discussing torsional stiffness in ship’s hulls with one of our intern engineers and pointed out a torsional stiffness problem with a certain hull design section since it could not inscribe a decent sized circle.
I expected it to be a comment that would be confusing to a young engineer and proceeded to explain that torsional stiffness is related to gyradius which is powerfully related to radius and radius is related to circles. Inherently the stiffest shape in torsion is a circle and the closer to a circle the better.
A square tube of a certain circumference is much stiffer in torsion than a rectangular tube of the same circumference and that can be confirmed by noting that the inscribed circle in the square tube is bigger than the inscribed circle in the rectangular tube.
This was explained to me when I was a young engineer and it has stood me in very good stead in quickly assessing torsional issues.
While I was explaining this to the intern, he started googling inscribed circles and torsional stiffness and came up with … nothing.
We did find lots of equations for torsional stiffness of thin-walled tubes, and the online version of “Roark’s Formulas for Stress and Strain” even made a marginal reference to inscribed circles in a few of its torsional equations, but I could find absolutely nothing that made mention of my very useful engineering rule of thumb.
This made me wonder how many other neat engineering tricks will disappear in our world of CAD, FEA and AI.
I have mentioned “Beam is Cheap” in a prior column, but even this well-known axiom is not readily found on the internet. As a matter of fact, the only way I could find a reference to “Beam is Cheap” in the context of ship design was to google “Rik van Hemmen Beam is Cheap”.
Another rule that I find extremely useful is that 44 ft. is the maximum length that is needed for a seaworthy oceangoing sailboat. Smaller is possible, but once you hit 44 feet you are adding luxury instead of seaworthiness. I googled: “Smallest reasonable size for an ocean crossing sailboat” and there were a lot of articles that discussed sailboat size. They often came up with smaller sizes, but interestingly nobody advocated anything longer than 45 feet, a subtle confirmation of that truth.
In the spirit of service to the engineering profession I will provide two more engineering truths.
The first one relates to mast placement on sloops. As a young designer I was working for Johan Valentijn and was laying out a new sailboat design and asked him if he had any good references on mast placement. Johan said: “Don’t bother. Put it on station four.”
At Valentijn Inc., all boat stations were 10% of the bow to rudder stock, so it ends up at 40% waterline. As a young pinhead engineer that confused me because he had barely seen the design. “Uh, how do you know Johan?”
“Because all boats that I design have good balance with the mast at station four.” He then explained that when he worked at Sparkman & Stephens, they always struggled with helm balance on boats (Yes, even S&S designs were not always perfect out of the box) and he simply took all S&S designs and plotted mast station against weatherhelm and only boats with the mast at station 4 had perfect helm.
Johan said it made no difference if the boat was a cutter or fractional rig boat, and even claimed that it worked for Bermuda rigged yawls. I have never designed a yawl (quite frankly, who would anymore?) so cannot answer for that, but even today when I look at very modern sailboats, I keep seeing station 4. When I google “mast location for a sloop” I do get a reference to station 4 for masthead sloops but not for fractional rigs where they advocate station 3, which, to me, looks very far forward and may work for a dinghy (where body placement can control the boat), but I would have no confidence in it for a keelboat.
Then there is the hull speed equation for slender hulls. The standard equation for hull speed in knots is familiar to just about every naval architect:
- Hull speed = 1.34 x Square Root (L)
Where L is the waterline length in feet.
However, for slender hulls I have seen hull speed defined as:
- Slender Hull speed = L/3B x Square Root (L)
Where B is the waterline beam in feet.
It basically says that if the Length to Beam ratio is greater than 4, hull speed will go up.
I copied the equation from a really nice book on multihull design (of which I do not remember the title and author name) and then somebody “borrowed” the book. It was never returned, and all I had was the equation which I happened to copy into a presentation on Zen and Naval Architecture that survives. I have often searched for the origin of this equation, and even sent intern engineers on searches, but this equation is not referenced anywhere and even marine designers older than me do not recognize it. Nevertheless, it is very helpful, and in my experience, provides very useful results when playing with slender hull designs.
These hull speed equations basically show the point where a hull hits the classic Froude number wall with sharply increasing wave drag. To go faster the hull has to transition to planing mode, but since planing is not terribly efficient for slender hulls, it shows at what speed there is a trade off point between planing hulls and slender hulls.
It does not provide hard numbers, but it is excellent for comparisons and trade offs and to prevent a designer from becoming confused about interlocking design issues.
Just putting these four concepts together will provide a designer with a quick frame of reference:
“Let me design an ocean crossing sailboat that is 44 feet long and skinny to get better non-planing speed, but I have to put the mast at station 4 and make sure I keep sufficient torsional stiffness in that small cross section.”
These are just four variables in the hundreds of variables that come into play with boat design, but reducing variables simplifies the overall equation and will result in better solutions.
Most of all, these tricks are extremely helpful in eliminating incorrect solutions and therefore should not be forgotten or we will be doomed to repeat the mistakes made by our predecessors. I just wish there were a way to transfer that engineering knowledge more efficiently. It appears the internet, despite its many engineering benefits is not well suited for it.
For each column I write, MREN has agreed to make a small donation to an organization of my choice. For this column I nominate the Herreshoff Museum. In my mind one of the best places to preserve engineering realities.